効率よく合格点が取れるように、捨て問題を×(時間がかかりすぎるか難しい問題)、できれば正解したいものを△、絶対に落としてはいけないものを〇という風に設定して解説してみました。
目標は70~75点に設定。合格点である60点プラス10~15点(2~3問)は頑張って正解し、残り5~6問は全く解けなくても大丈夫という感じで臨みましょう。
問2:〇
目標時間 5分
【問題】
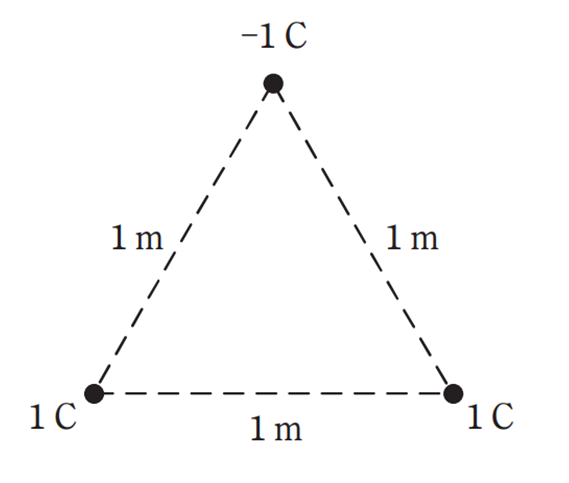
真空中において,図に示すように一辺の長さが \(1m\) の正三角形の各頂点に \(1C\)又は \(-1C\) の点電荷がある。
この場合,正の点電荷に働く力の大きさ\({F_1}\) [\({N}\)]と,負の点電荷に働く力の大きさ\({F_2}\) [\({N}\)]の比\({F_2}\) / \({F_1}\) の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(\sqrt{2}\) (2) \({1.5}\) (3) \(\sqrt{3}\) (4) \({2}\) (5) \(\sqrt{5}\)
【解説】
解答:(3)
クーロンの法則を用いて点電荷に加わる力を求める問題です。
ラッキー問題とまでは言いませんが、落ち着いてベクトルを書くことができれば難なく正答出来ると思います。
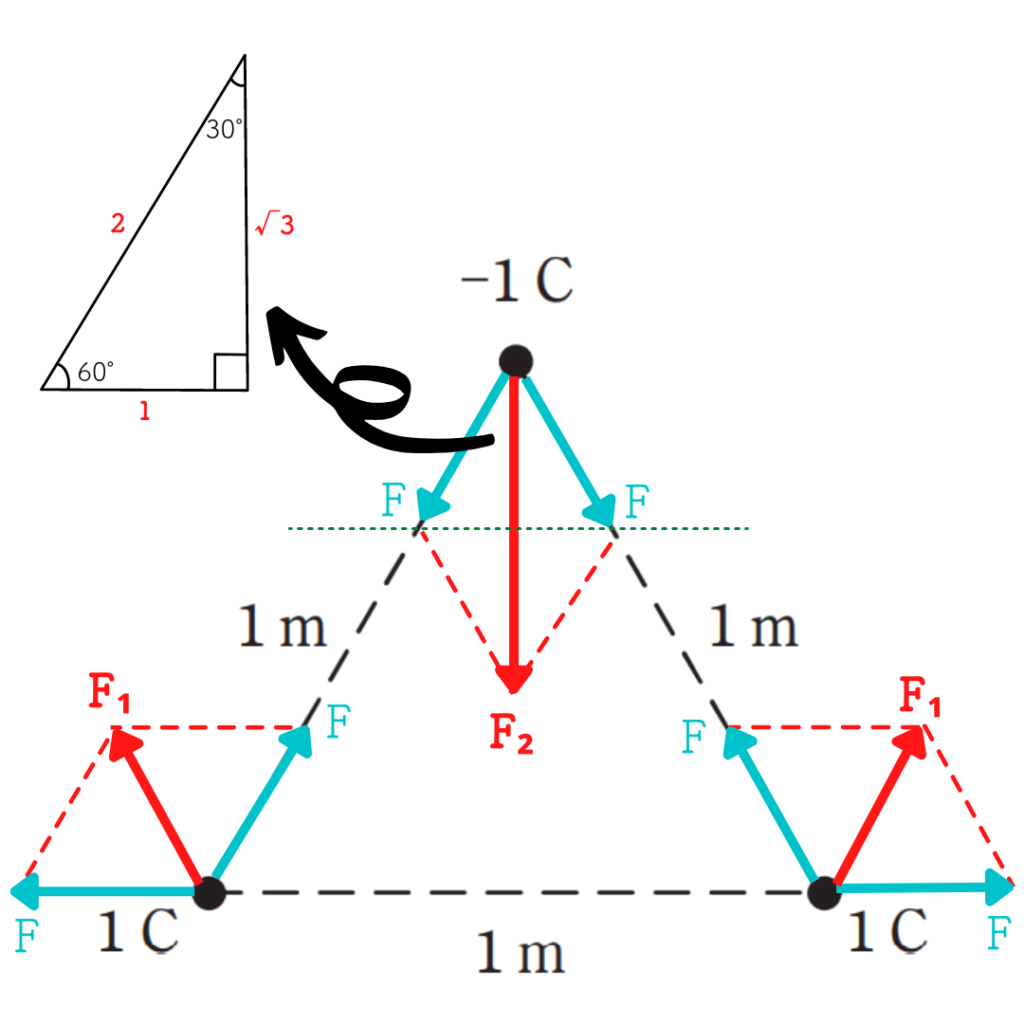
図1のように各点電荷に加わる力を書いてみましょう。
本問の場合、真空中におけるクーロンの法則の公式
\(\displaystyle{F}=\frac{{Q_1}{Q_2}}{4\pi ε_0r^{2}}\)
こちらを使って計算しなくても解けますが、重要公式なので覚えておきましょう。
また、本問に数値を代入して\(F\)の値を求めると
\begin{eqnarray}F&=& \frac{1\times1}{4\pi ε_0\times1^{2}}\\ &=&\frac{1}{4\pi ε_0}[N]\end{eqnarray}
となります。
図1のとおり、正三角形の性質より\({F}\)と\({F_1}\)は大きさが等しくなる。
次に、\(-1C\)の点電荷に加わる力も同様に\(F\)となり(正電荷と負電荷の場合は引力【引き合う力】、同符号の電荷同士だと斥力【反発する力】が働く)、ベクトルを合成すると\(F_2\)となる。
\(F_2\)の大きさは図1のように三角形の比を用いると、
\begin{eqnarray}F_2&=& F\times\frac{\sqrt3}{2}・2\\ &=&\sqrt3F[N]\end{eqnarray}
となる。したがって、\({F_1}\) [\({N}\)]と\({F_2}\) [\({N}\)]の比、\({F_2}\) / \({F_1}\) は\({F=F_1}\)であるから、
\begin{eqnarray}\frac{F_2}{F_1}&=& \frac{\sqrt3F}{F}\\ &=&\sqrt3\end{eqnarray}
と求められる。


コメント