効率よく合格点が取れるように、捨て問題を×(時間がかかりすぎるか難しい問題)、できれば正解したいものを△、絶対に落としてはいけないものを〇という風に設定して解説してみました。
目標は70~75点に設定。合格点である60点プラス10~15点(2~3問)は頑張って正解し、残り5~6問は全く解けなくても大丈夫という感じで臨みましょう。
問3:△
目標時間 7分
【問題】
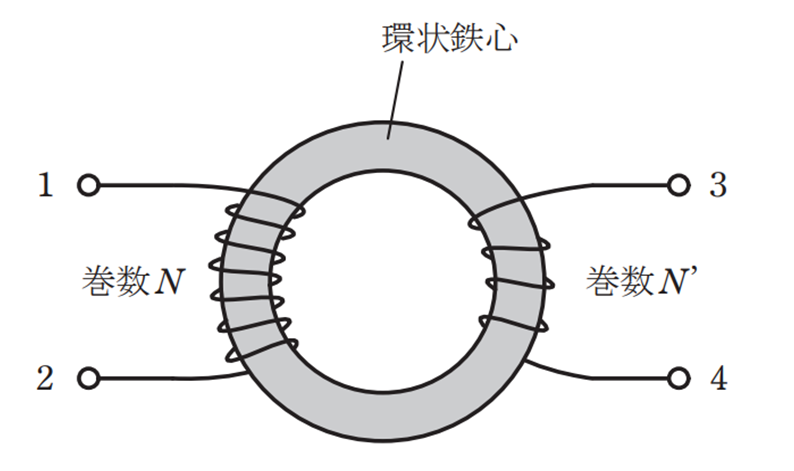
図のような環状鉄心に巻かれたコイルがある。
図の環状コイルについて,
・端子 \(1-2\) 間の自己インダクタンスを測定したところ,\(40[mH]\) であった。
・端子 \(3-4\) 間の自己インダクタンスを測定したところ,\(10[mH]\) であった。
・端子 \(2\) と \(3\) を接続した状態で端子\(1-4\) 間のインダクタンスを測定したところ,\(86[mH]\) であった。
このとき,端子 \(1-2\) 間のコイルと端子\(3-4\) 間のコイルとの間の結合係数\(k\) の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.81 (2) 0.90 (3) 0.95 (4) 0.98 (5) 1.8
【解説】
解答:(2)
相互インダクタンスと、合成インダクタンスの両方の公式を覚えていないと解けないので、けっこう難易度が高い問題だと個人的には思います。
(ちなみに僕は公式をド忘れして初見では解けませんでした…汗)
①相互インダクタンス\(M\)
自己インダクタンス\(L_{1}\)と\(L_{2}\)がある時、相互インダクタンス\(M\)は、
\(M=k\sqrt{L_{1}L_{2}}\)
となり、\(k\)は結合係数と呼ばれ \(0≦k≦1\) となります。
②合成インダクタンス\(L_{0}\)
磁束が強め合う(磁界の向きが同じ)時、和動接続と呼ばれ以下の公式となります。
\(L_{0}=L_1+L_2+2M\)
磁束が弱め合う(磁界の向きが反対)時、差動接続と呼ばれ以下の公式となります。
\(L_{0}=L_1+L_2-2M\)
相互インダクタンスを\(M\)、端子\(1-2\)間の自己インダクタンスを\(L_{12}=40[mH]\)、端子\(3-4\)間の自己インダクタンスを\(L_{34}=10[mH]\)、結合係数を\(k\)とすると、
\begin{eqnarray}M&=& k\sqrt{L_{12}L_{34}}\\ &=&k\sqrt{40\times10}\\ &=&20k[mH] \end{eqnarray}
となります。
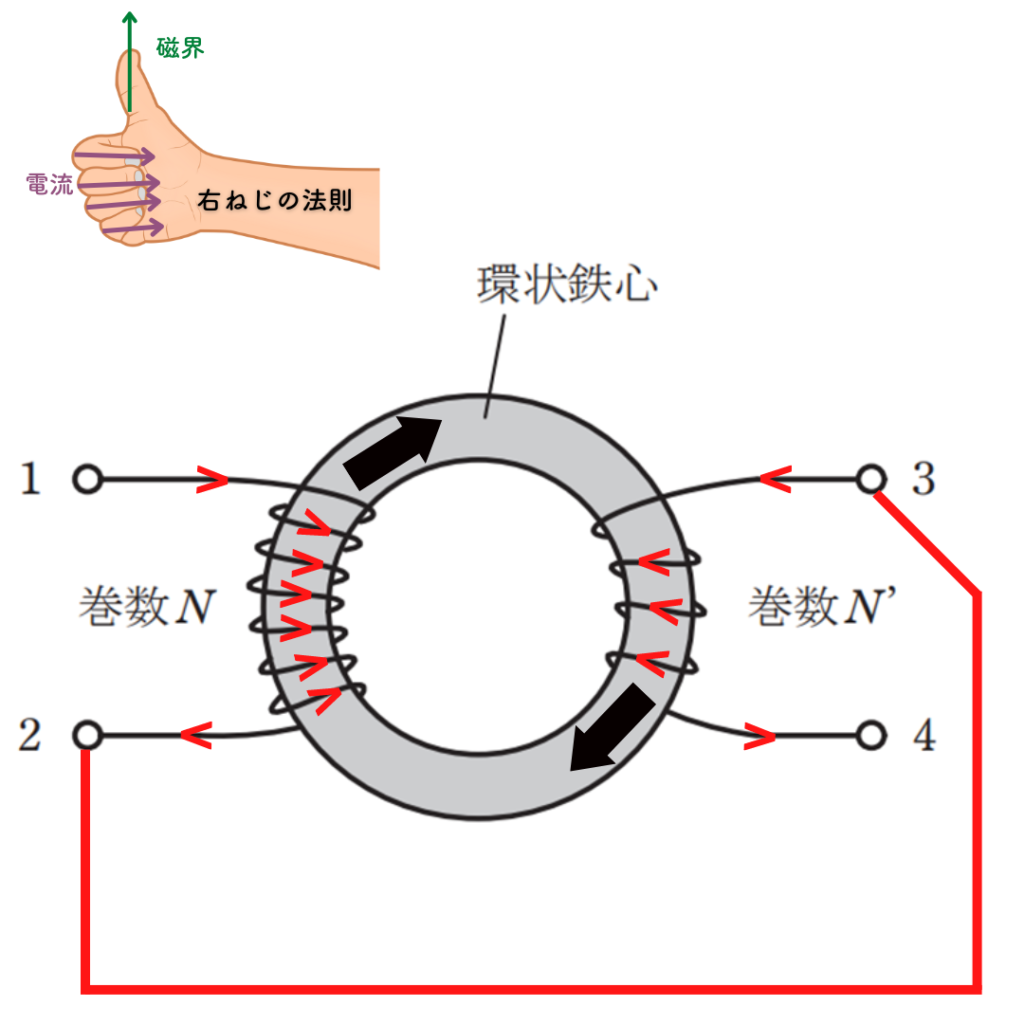
また、図1のように端子\(2-3\) 間をつないだ場合は自己インダクタンス\(L_{12}\)と\(L_{34}\)が接続されたことになり、この場合、右ねじの法則を用いて\(L_{12}\)と\(L_{34}\)の合成インダクタンスが和動接続か差動接続かを見極める必要があります。
図1のように右手を握って親指を立てて、赤の矢印が電流、黒太矢印が磁界と置くと\(L_{12}\)と\(L_{34}\)が生み出す磁界は同じ時計回りになります。よってこの場合は和動接続だと判断できます。
合成インダクタンスを\(L_{0}\)とすると、
\begin{eqnarray}L_0&=&L_{12}+L_{34}+2M\\ 86&=&40+10+2・20k\\ 40k&=&36\\ k&=&0.90 \end{eqnarray}
という風に、結合係数\(k\)が求められます。


コメント